A Centroid is defined as the point where the three medians of the triangle met or intersect each other. You can also visually estimate that the area facts given above are true.
- Instructor So the goal of this video is to prove that the three medians of a triangle always intersect at one point which is pretty interesting because you would expect two different lines with different slopes to intersect in one point but three lines intersecting in one point is pretty neat.
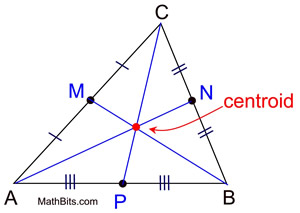
. There are a number of theorems that we need to look at before we doing the proof. What is a segment called that joins a vertex to the opposite side so that it is perpendicular to that side. The medians meet in an interesting point but its not equidistant from the vertices because the medians always meet inside the triangle.
We have not only proved our theorem but we have learned something about where this point is located. It is also defined as the point of intersection of all the three medians. Common point of triangle medians Theorem.
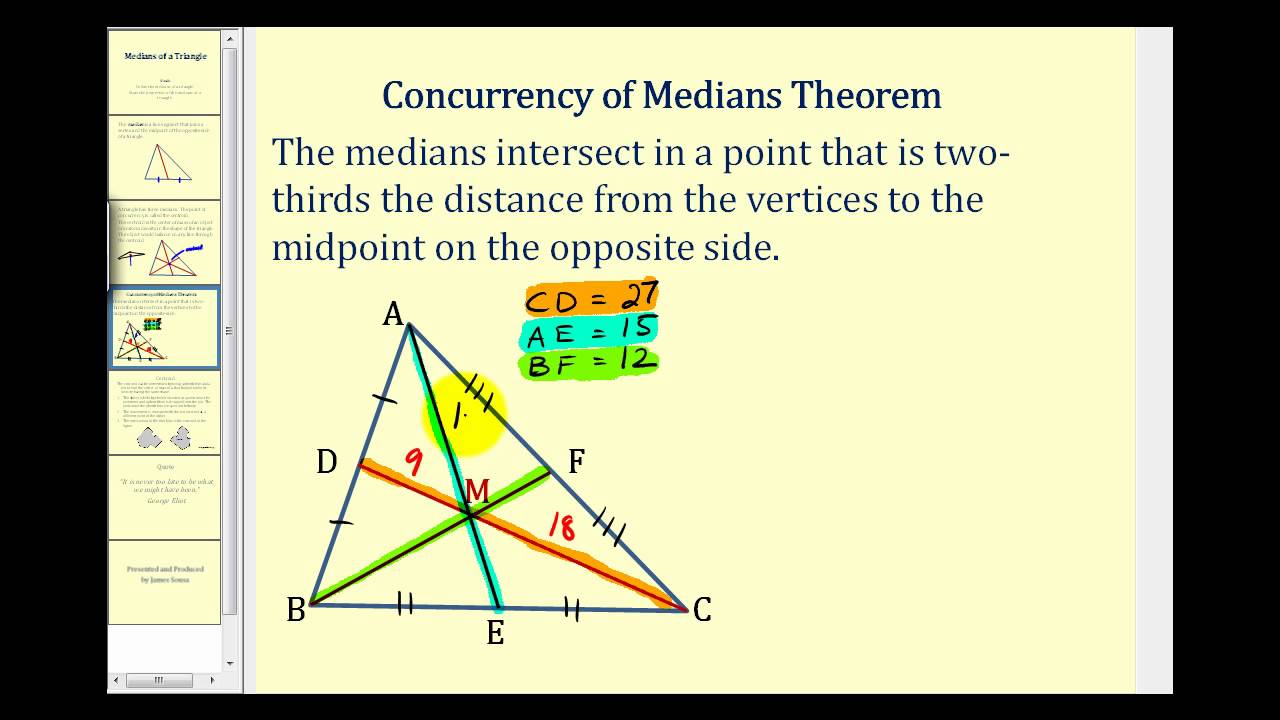
Symbols If P is the centroid of TABC then AP 5 2 3AD BP 5 2 3BF and CP 5 2 3CE. Is it possible for a line to intersect No sides of a triangle. What is the point called where three medians of a triangle intersect.
The centroid divides each of the medians in the ratio 21 which is to say it is located ⅓ of the distance from each. The unique point equidistant from the vertices is the center of the circle passing through them so. It is possible for the orthocenter to occur on the triangle on the interior of the triangle or on the exterior of the triangle orthocenter The angle formed by the two equal sides of.
The idea of this proof is not correct. The point where the three medians of a triangle intersect is called a centroid from the Latin word centrum--. Every triangle has exactly three medians one from each vertex and they all intersect each other at the triangles centroid.
Answer 1 of 2. We know that medians trisect each other and that trisect point is called centroid. The median of a triangle theorem states that the medians of a triangle intersect at a point called the centroid of the triangle which is two-thirds of the distance from the vertices to the midpoint of the opposite sides.
The median is a line that joins the midpoint of a side and the opposite vertex of the triangle. Therefore the three medians intersect at a point. The concept of a.
What is the point called where three altitudes of a triangle intersect. Convince yourself that the three medians gray lines always intersect at a single point. In a triangle ABC if and then is equal to 80 40 60 20 60 Views Answer 76.
P B A C D F E THEOREM 49 The following theorem tells you that the three medians of a triangle intersect at one point. The point of intersection of all three medians is called the centroid of the triangle. What is the intersection of three medians in a triangle.
Words The medians of a triangle intersect at the centroid a point that is two thirds of the distance from each vertex to the midpoint of the opposite side. CENTROID concurrent medians. In the case of isosceles and equilateral triangles a median bisects any angle at a vertex whose two adjacent sides are equal in length.
Adjust the triangle above by dragging any vertex. We say that they are concurrent. X and Y are the mid-points of sides of AB and AC of ΔABC.
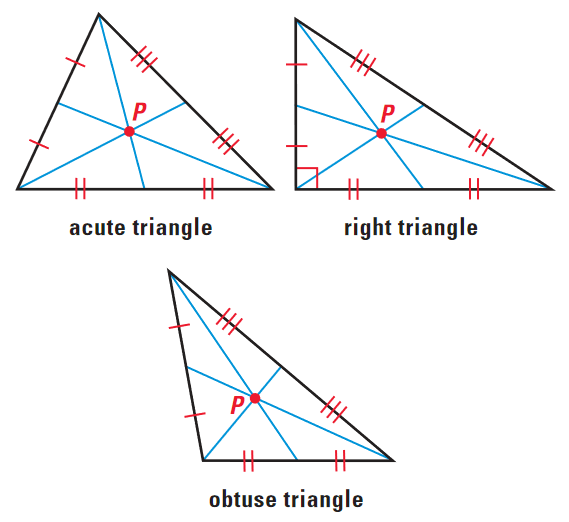
Therefore the three medians of any triangle meet at a common point known as the centroid that cuts each median into a ratio of 2. The centroid is the balancing point of a triangle. The medians of a triangle intersect each other in the ratio 21.
But others have not been honest enough. The intersection point of all the 3 medians of a triangle is called Centriod of the triangle. Median - median is the line segment joining vertex of the triangle and the mid- point of the opposite side The point.
Median of a triangle a point in which the three altitudes of the triangle intersect. If BC XY 12 units then BC - XY is. What is the intersection of the three medians of a triangle.
Here I will simply state the theorems formal proofs are omitted but are part of secondary school mathematics 1. Moreover AG 2GD BG 2 GE and CG 2GF. The coordinates of the of the centroid are basically the average of the coordinates of the vertices of the triangle.
The three median of any triangle are concurrent. The point of intersection of all the three medians of a triangle is called its Orthocentre Incentre Centroid Circumcentre 53 Views Switch Flag Bookmark 75. The medians of a triangle are the segments drawn from the vertices to the midpoints of the opposite sides.
The three medians of a triangle intersect at a single point. 8 units 4 units. The three corners of the triangle trace the three medians of the triangle.
Their point of intersection is called the point of concurrence of the medians. When three medians of a triangle meet at a point it is called a. The medians are concurrent.
Centroid If you draw all three medians they will intersect at one point called the centroid. Referring to the figure below prove that three medians of triangle ABC intersect at the terminal point P of the vector The point P is called the centroid of. Please dont take this harshly -- I think its a very nice idea.
This means that if you were to cut out the triangle the centroid is its center of gravity so you could balance it there. The three medians divide the triangle into 6 smaller triangles that all have the same area even though they may have different shapes. Thus A centroid is the intersection of three medians in a triangle.
The point in which the three medians of the triangle intersect is known as the centroid of a triangle. A median of a triangle is a segment joining a vertex t the midpoint of the opposite side. The centroid of a triangle is the point of intersection of its medians the lines joining each vertex with the midpoint of the opposite side.
It is also known as the center of gravity of the triangle. That is if ABC and D E F are the midpoints of the sides opposite A B C respectively then the segments AF BD CE all intersect in a common point G. The distance from each vertex of a triangle to the point of concurrence of its medians is two-thirds of the total length of the median from this vertex.

Centroid Mathbitsnotebook Geo Ccss Math

Geometry Show That The Three Medians Of A Triangle Are Concurrent At A Point Mathematics Stack Exchange
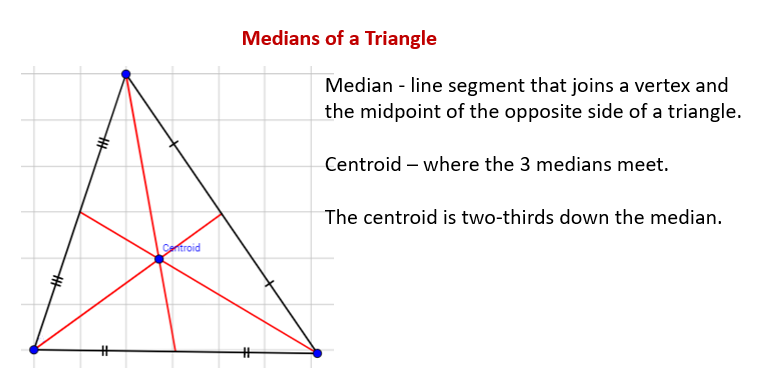
Construct The Median Of A Triangle Solutions Examples Worksheets Videos Games Activities

Proving Triangle Medians Intersect At A Point Video Khan Academy
Constructing A Triangle With Three Medians
%20of%20a%20Triangle/TriMedEx01.gif)

0 comments
Post a Comment